2. Der Doppler-Effekt
Der Doppler-Effekt, ist etwas, das uns tagtäglich begegnet und für die Wissenschaft in der Vergangenheit und heute eine große Rolle spielt. Was verbirgt sich nun hinter diesem Effekt?
Den Doppler-Effekt hat jeder von uns schon einmal auf die eine oder andere Weise erlebt. Ein beliebtes Beispiel zur Erklärung ist das Heulen der Sirene eines Krankenwagens, der an einer Person (nennen wir diese Person Hans) vorbeifährt.
Nun, unser Hans geht an der Straße entlang und bleibt vor einer Ampel stehen. In diesem Moment rast mit hoher Geschwindigkeit ein Krankenwagen auf die Ampel zu und fährt an Hans vorbei. Hans hat sich, während der Krankenwagen vorbeigefahren ist, nicht weiterbewegt, aber ihm ist etwas besonderes aufgefallen.
Wenn der Krankenwagen auf Hans zufährt, erhöht sich der Ton der Sirene, und nachdem der Wagen an Hans vorbei ist, wird der Ton tiefer. Unser Hans fragt sich darauf, warum ändert sich der Ton der Sirene?
Christian Doppler hat eine Antwort auf die Frage von Hans gefunden, auch wenn das nicht Doppler’s Hauptanliegen war.
Zuerst werde ich kurz etwas zu der Entdeckung des Effektes durch Christian Doppler erklären und danach die Grundzüge erklären.
1842 sagte Doppler diesen Effekt voraus. Er hatte ihn nicht bewiesen, sondern zunächst eine Theorie aufgestellt, die 1845 von Christoph Buys-Ballot experimentell bewiesen wurde.
Doppler hat mit seiner Theorie einen grundlegenden Effekt theoretisch beschrieben und erklärt. Eigentlich hatte er nicht vor, zu erklären, weshalb sich ein Ton mal tiefer und mal höher anhört, sondern wie die unterschiedlichen Farben der Sterne zu Stande kommen.
Heute ist klar, dass er dabei mit seiner Theorie, die Farbe der Sterne durch ihre Eigenbewegung zu erklären, falsch lag, da die Oberflächentemperatur und die Oberfläche des Sterns die Farbe und die Helligkeit am Himmel bestimmen.
Aber nun zurück zu Hans' Beobachtung, die man durch den Doppler-Effekt genau erklären kann.
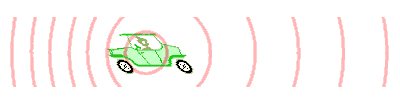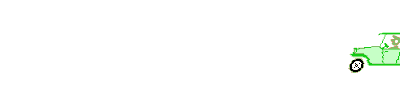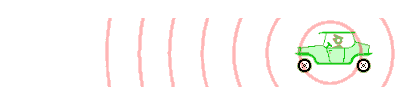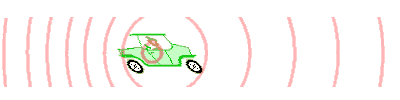
Die Grafik zeigt, wie sich die Schallwellen von dem Wagen ausbreiten. Wenn der Wagen sich nicht vorwärts bewegt, breiten sich die Wellen gleichmäßig in alle Richtungen aus. Wie deutlich zu erkennen ist, verändern sich die Abstände der Wellen, wenn sich der Wagen in Bewegung setzt. Die Wellen vor dem Wagen liegen dichter zusammen, das heißt, die Wellenlänge wird kürzer. Hinter dem Wagen liegen sie dagegen weiter auseinander als bei dem stehenden Fahrzeug am Anfang.
Um zu erklären, weshalb sich die Tonhöhe der Sirene ändert, muss man wissen, wie die Tonhöhe zustande kommt und welche Faktoren den Ton verändern. Dazu nun eine Formel, die den Zusammenhang zwischen Wellenlänge und Frequenz berechnet. Bei Schallwellen entspricht die Frequenz der Tonhöhe.
λ ist hier die Wellenlänge
c ist die Ausbreitungsgeschwindigkeit (hier die Schallgeschwindigkeit)
ƒ ist die Frequenz
Da sich die Ausbreitungsgeschwindigkeit c nicht ändert (die Schallgeschwindigkeit (c) ist eine feste Ausbreitungsgeschwindigkeit bei Schallwellen), wird mit größerer Wellenlänge λ die Frequenz verringert und umgekehrt.
Um die Änderung in der Wellenlänge zu berechnen, gibt es eine weitere Formel:
v ist hierbei die Geschwindigkeit des Krankenwagens
Δλ ist die Änderung der Wellenlänge
Wenn der Krankenwagen sich also auf Hans zubewegt, dann verkürzt sich die Wellenlänge und die Frequenz steigt entsprechend; dadurch ist der Ton erhöht. Ist der Wagen vorbei, vergrößert sich die Wellenlänge und die Frequenz wird niedriger, der Ton erscheint uns tiefer.
Bei einer elektromagnetischen Welle, funktioniert es genauso wie bei Schallwellen. Die Veränderung der Wellenlänge oder der Frequenz wird bei elektromagnetischen Wellen meist im Spektrum des aussendenden Objekts gemessen. Anhand dieser Verschiebung kann man berechnen, mit welcher Geschwindigkeit sich das Objekt von uns entfernt oder auf uns zu bewegt. Diese Verschiebung kann sowohl in den roten als auch in den blauen Bereich des Spektrums erfolgen und zeigt, ob sich das Objekt von uns entfernt (Rotverschiebung) oder sich auf uns zu bewegt (Blauverschiebung).
Dazu benutzt man die Doppler-Formel:
Δλ ist die Wellenlängenänderung (Δλ = λ − λ0)
λ0 ist die ursprünglich ausgesandte Wellenlänge
λ ist die Wellenlänge
v ist die Geschwindigkeit des Objekts
c ist bei elektromagnetischen Wellen die Lichtgeschwindigkeit, bei Schallwellen dementsprechend die Schallgeschwindigkeit
Die Unbekannte ist die Geschwindigkeit v, denn c (ist eine bekannte Größe), Δλ und λ sind auf jeden Fall gegeben, da es die Komponenten sind die gemessen werden bzw. bekannt sind. Δλ ist die Änderung der Wellenlänge, die gemessen werden muss, beispielsweise mit einem Teleskop, wenn man anhand von Spektrallinien die Radialgeschwindigkeit eines Sterns ermitteln möchte.
Mit Hilfe des Doppler-Effektes werden mittlerweile auch Planeten außerhalb unseres Sonnensystems aufgespürt, da man anhand der spektralen Verschiebung Informationen ableiten kann, die Aufschluss geben können über bestimmte Radialbewegungen, die der Stern aufgrund von gravitativen Einflüssen macht. Die gleiche Methode wird auch bei der Suche nach spektroskopischen Doppelsternen angewandt.
Der Doppler-Effekt wird übrigens auch genutzt, um bei Radarfallen (Dopplerradar) die genaue Geschwindigkeit zu ermitteln.
weitere Informationen:
auf wikipedia
bei René Kubach
bei Jürgen Giesen
